The autocorrelation function is the ratio of the kth sample autocovariance to the sample covariance, i.e.,
A plot of rk against lag k is evaluated for discernible patterns, relationships, and absolute values (e.g., close to zero).
The R package RND computes the implied volatility for a Call option. A sample usage is given as below.
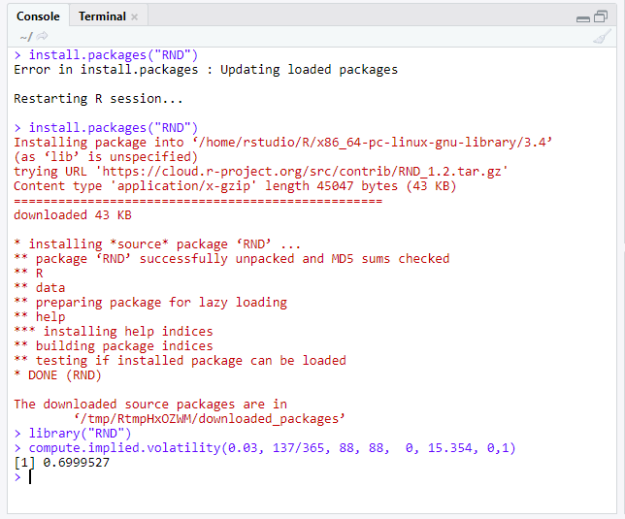
The implied volatility based on the Black-Scholes model differs from realized volatility in that the latter is a retrospective estimate of price, while the former provides insight into the future.
Realized volatility can be derived from more traditional approach like standard deviation and GARCH models. Implied volatility, on the other hand, must be found numerically because the Black-Scholes formula cannot be solved for phi in terms of other parameters. A previous installment provides more mathematical details in TI Nspire.
The Blockchain is expected to be the revolutionary technology to take the centre stage in our society where the traditional ledger system once dominates, from bitcoin that emerged in the finance sector to fields where transactions are dependent on authenticity, be it a paper document from bank, an import / export data exchange, or even documents in judicial systems, it is important to understand the principles of its fundamental roots in cryptography.
For example, to ensure the rightful spending of currency in bitcoins, there are a lot of technology being in place on the virtual money market. One being the Elliptic Curve Cryptography that is based on mathematics to ensure the identity of parties involved in any bitcoin transactions.
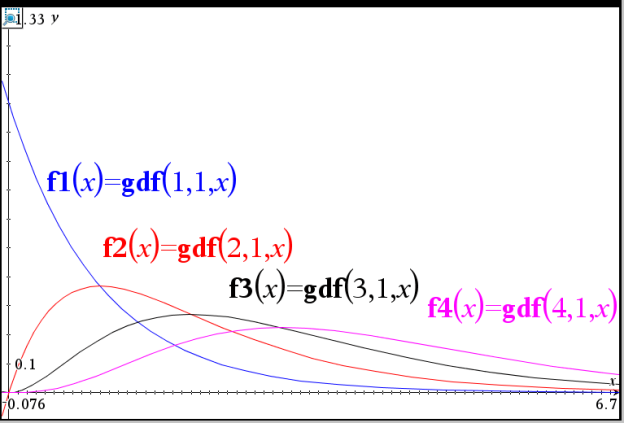
The gamma function is not a built-in function in the TI Nspire. Nevertheless this function can easily be defined and used for visualising the gamma probability distribution function.
gmgolem 