The Hessian is a matrix composed of second order partial derivatives of function. The Nspire does not provide built-in function for this, and a handy function below achieve the same purpose, although it is good for a 2 x 2 matrix.
The HP Prime provided built-in function for Hessian matrix.
In TI Nspire, matrix multiplication can be accomplished in the Calculator page. The process is intuitive and easy with the visual templates.
Firstly use the matrix template to define one:
Then simply do multiplication after filling in the matrix elements.
Doing so in Excel required the use of the MMULT() function. A little trick is needed for this function for returning answer in array format – by pressing CTRL+SHIFT+ENTER at the same time after inputting the function for the cells selected as output array.
First step, fill in the matrix with the elements into respective cells.
Mark the output region to use the array function. In this example it is also a 3×3 matrix.
Apply the MMULT() function on the upper left corner cell of the region selected.
The trick is here, when finished typing in the function, press CTRL+SHIFT+ENTER instead of just ENTER. The answer from the function will then be populated in the selected cells, and the formula will be displayed with curly brackets enclosed, like {=MMULT(B2:D4,F2:H4)}.
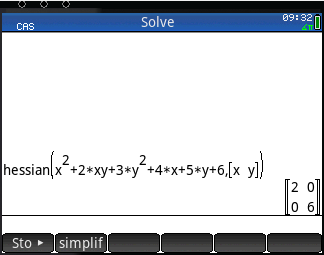
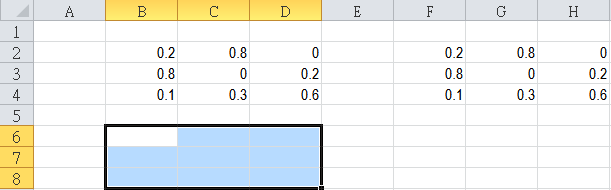
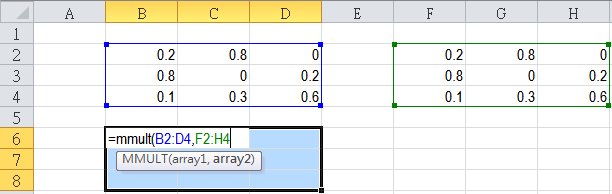
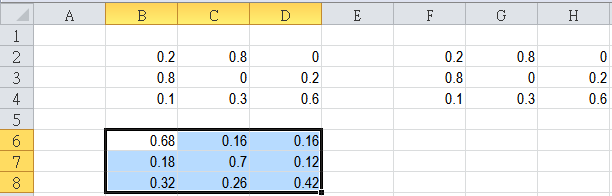
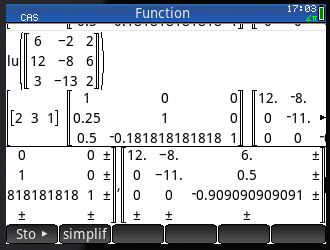
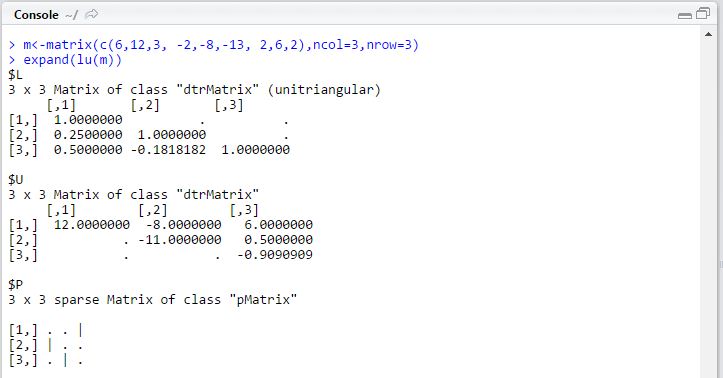
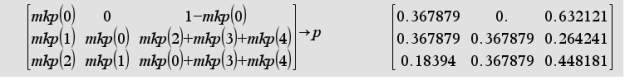In calculation for Markov chain, matrix setup can be complicated evn with the user-friendly interface on the TI Nspire. The built-in function like identity(), constructMat() etc are useful on specific cases.
For Markov chain calculation, the model setup in terms of matrix sometimes get quite complicated and demanded a few exceptions from the built-in function mentioned above that are geared towards common linear algebra.
The example below attempts to simply the construction of the Markov model by use of piece-wise functions in building matrix. The problem to solve in Markov process is on a stock resupply problem, where an imaginary shop keeps stock of 1 to 3, and replenish on each day only when all stock is exhausted. Poisson distribution is assumed on the demand side.
Firstly a function called markov_prob is created, which takes the demand as variable and return the corresponding Poisson distribution. Note that how the function handle probability for demand greater than 3. A short-hand function mkp() is created afterwards to ease reading in the matrix.
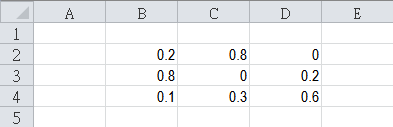
When the function is defined, the Markov model can be formulated in a new 3 x 3 matrix created using the template. It is sometimes not easy to define state transition function as in this example problem. Therefore, the shorthand function just created will help in filling in the states as matrix elements. For example, P11 means the stock next day (Sx+1) equals stock today (Sx) which is 1, and that means the demand is zero, and thus mkp(0). There are some curve ball like P12, where Sx+1 > Sx which is not possible, since that means the shop has more stock the next day for any day with non-zero stock (i.e. negative demand), and thus the probability is zero.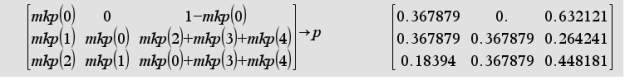
After setting up the Markov model, the equilibrium distribution can be deduced. The below is one of the methods using Nelder-Mead algorithm.
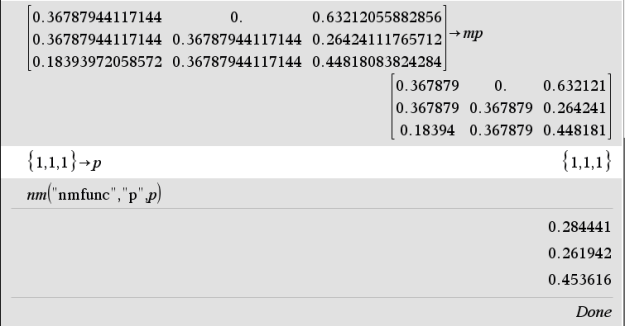
Based on this model, more figures can be deduced for decision making on fine tuning stock keeping strategy.
High-end calculators are capable to compute the LU decomposition of matrix. TI Nspire CAS and HP Prime are no exception. The calculations for them are listed below and compared with R.
TI Nspire CX CAS
HP Prime
R
gmgolem 