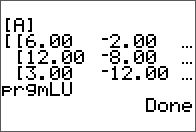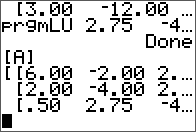The Julia language released version 1.0 earlier this month (August 8th 2018). Julia is aimed at statistics, computation, and data science with capabilities of numerical analysis in a high level dynamic programming language. JuliaBox provides online workspace to test drive this exciting tool, as shown below an LU decomposition example.
As an extension to a previous entry on doing LU decomposition in Nspire and R, the TI-84 is covered here. There is no built-in function like in the Nspire for this, but there are many programs available online, with most of them employing a simple Doolittle algorithm without pivoting.
The non-pivoting program described here for the TI-84 series is with a twist. No separate L and U matrix variables are used and the calculations are done in place with the original input matrix A. The end result of both L and U are also stored in this input matrix. This is made possible by the property of the L and U matrices in this decomposition are triangular. Therefore, at the little price of some mental interpretation of the program output, this program will take up less memory and run a little faster than most simple LU decomposition programs online for the same class of calculator. From a simple benchmark with a 5 x 5 matrix, this program took 2 seconds while another standard program took 2.7 seconds.
The input matrix A.
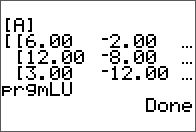
Results are stored in the same matrix.
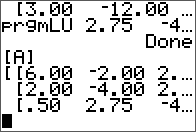
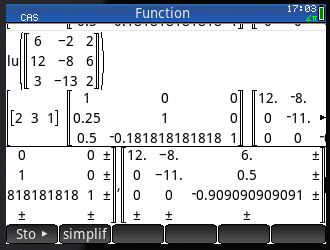
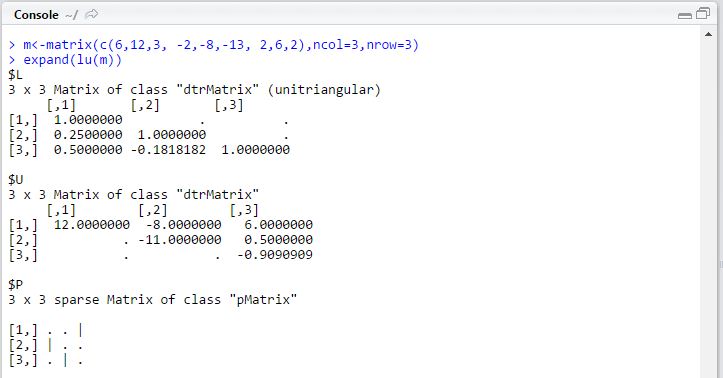
L, U, and verification.
High-end calculators are capable to compute the LU decomposition of matrix. TI Nspire CAS and HP Prime are no exception. The calculations for them are listed below and compared with R.
TI Nspire CX CAS
HP Prime
R
gmgolem 