With matrix capable calculator, simplex algorithm for common maximization problem can be solved easily like in the TI-84.
The Casio 9860GII is also equipped with equivalent matrix operations to solve the same problem.


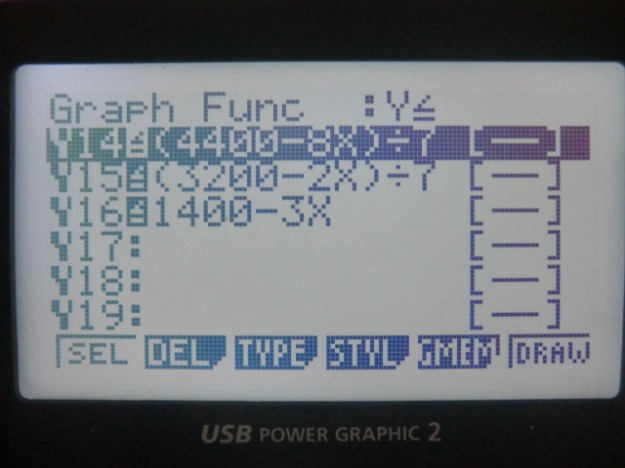
With matrix capable calculator, simplex algorithm for common maximization problem can be solved easily like in the TI-84.
The Casio 9860GII is also equipped with equivalent matrix operations to solve the same problem.




In last installment, the Casio overclocking utility Ftune2 improved the speed performance of a Nelder-Mead program by 4.5 times. For standard calculations, more impressive results are obtained from this nice utility. In this test, the standard normal distribution function is applied in the Casio fx9860GII Equation Solver and the task is to find the Z variable (as “T” in the below screen), given the cumulative probability distribution of 0.9 (as “A” in the below screen).
A=1÷(√(2π))×∫(e^(-X²÷2),-999,T)
In other words, the solver’s task is to find Z from the given area of 0.9 as shaded in the below chart, which is obtained for verifying the solver’s result of 1.28155156 using the command
Graph Y=P(1.28155156).
And here is the result on speed performance:
00:38 No overclocking, back-lit OFF
00:40 No overclocking, back-lit ON
00:06 Overclocked 265.42 MHz, USB OFF, back-lit OFF
00:07 Overclocked 265.42 MHz, USB OFF, back-lit ON
00:05 Overclocked 265.42 MHz, USB ON, back-lit OFF
00:05 Overclocked 265.42 MHz, USB ON, back-lit ON
The performance gain by overclocking is 7.6 to 8 times, depending whether the back-lit is on for non-overclocked runs.
For the same equation solving by the TI Nspire using nsolve(), it took 01:30 to return a result of 1.28155156555.
However, using the built-in standard functions NormCD() for the Casio and normCdf() for the TI as below
Casio fx-9860GII A=NormCD(-999,T) TI Nspire nsolve(normCdf(-∞,x,0,1)=0.9,x)
both units return results instantaneously (Nspire returns 1.28155193868 while Casio returns 1.281551566).
The Nelder-Mead algorithm is a very versatile optimization technique that is easy to implement. Having covered on how such a program in the TI-nSpire can help in estimating GARCH parameters, fitting logistic regression and Gompertz curve, I have decided to give it a try on a Casio fx-9860GII. It will also be an interesting opportunity to see the comparison of how these two calculators perform.
Compared to the more sophisticated programming features available on the TI-nSpire, programming the Nelder-Mead using the Casio language on the fx-9860GII is quite a challenge. Variables are limited to 28 and only single alphabet variable name is supported. Extra porting efforts are needed to deal with array features which must be borrowed from the fixed 26 List and 26 Matrix memory, and lack of elseif construct (not a big deal usually but just required extra effort in porting programming especially for those with nested loops). Fortunately, the expression evaluation feature is present on the Casio which is an important part for a dynamic implementation of the algorithm, otherwise there will be a strong cohesion between the algorithm itself and the function it handles.
For a quick porting, the structure and variables of the original program from the TI-Basic are preserved without much adaptations except those that are required for the program to work on the fx-9860GII like changing variable names to single alphabets, mapping arrays into Matrices and Lists etc.
After exhausting almost all 28 variables and 10+ matrices, it is about time to do a speed comparison. As used previously to benchmark the same program on the TI-nSpire, the Rosenbrog function is used again. For a fair comparison, the same initial parameter set {10,10} will be used on both machines.
And the result on performance:
0:22 Nspire CX CAS
1:25 fx-9860GII (version with in-line objective function)
1:28 fx-9860GII (version with objective function as string variable)
It is not that bad for the clock speed from the Casio (no overclocking) and also worth mention is that no particular optimization was done during code porting, and also the fact that the program is in Casio BASIC which is an interpreted language with execution performance far below native C.
In next installment, exciting results on boosted performance by overclocking will be posted for the same algorithm on the same hardware.
All programming on the Casio was done on the real calculator. The keys are nice and soft. With a user-friendly and consistent menu system to code the program, porting an existing program is not as tedious as previously thought, but rather a pleasant journey to learn another calculator as well as a refreshment to the Nelder-Mead algorithm.